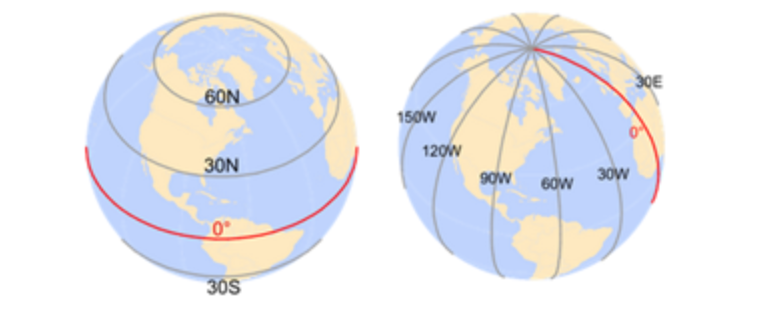
A Geographic Coordinate system (GCS) is a reference system for identifying locations on the curved surface of the earth. Locations on the earth’s surface are measured in angular units from the centre of the earth relative to two planes: the plane defined by the equator and the plane defined by the prime meridian (which crosses Greenwich England). A location is therefore defined by two values: a latitudinal value and a longitudinal value.
Source : https://mgimond.github.io/Spatial/chp09_0.html
A latitude measures the angle from the equatorial plane to the location on the earth’s surface. A longitude measures the angle between the prime meridian plane and the north-south plane that intersects the location of interest. In a GIS system, the North-South and East-West directions are encoded as signs. North and East are assigned a positive (+) sign and South and West are assigned a negative (-) sign.
In GIS, a GCS is defined by an Ellipsoid, Geoid and Datum.
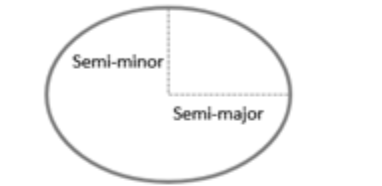
- Ellipsoid: Assuming that the earth is a perfect sphere greatly simplifies mathematical calculations and works well for small-scale maps (maps that show large area of the earth). However, when working at larger scales, an ellipsoid representation of earth may be desired if accurate measurements are needed. An ellipsoid is defined by two radii: the semi-major axis (the equatorial radius) and the semi-minor axis (the polar radius).
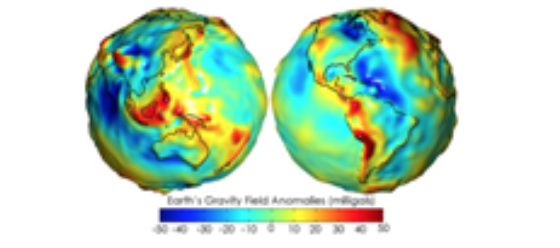
- Geoid: Representing the earth’s true shape, the geoid, as a mathematical model is crucial for a GIS environment. However, the earth’s shape is not a perfectly smooth surface. It has undulations resulting from changes in gravitational pull across its surface. These undulations may not be visible with the naked eye, but they are measurable and can influence locational measurements. Note that we are not including mountains and ocean bottoms in our discussion, instead we are focusing solely on the earth’s gravitational potential which can be best visualized by imagining the earth’s surface completely immersed in water and measuring the distance from the earth’s centre to the water surface over the entire earth surface.
Source: The COMET Program/ESA
- Datum: So how are we to reconcile our need to work with a (simple) mathematical model of the earth’s shape with the undulating nature of the earth’s surface (i.e., its geoid)? The solution is to align the geoid with the ellipsoid (or sphere) representation of the earth and to map the earth’s surface features onto this ellipsoid/sphere. The alignment can be local where the ellipsoid surface is closely fit to the geoid at a particular location on the earth’s surface or geocentric where the ellipsoid is aligned with the centre of the earth. How one chooses to align the ellipsoid to the geoid defines a datum.
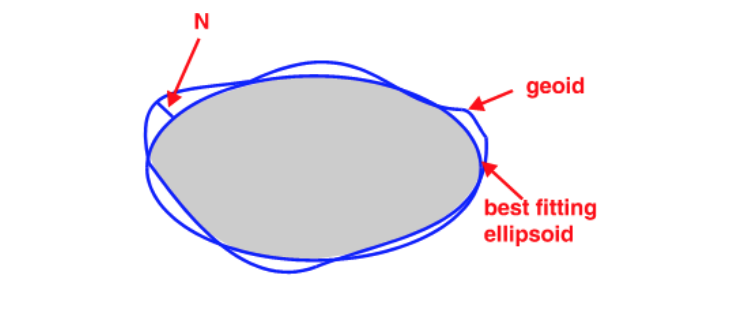
Source: The COMET Program/ESA
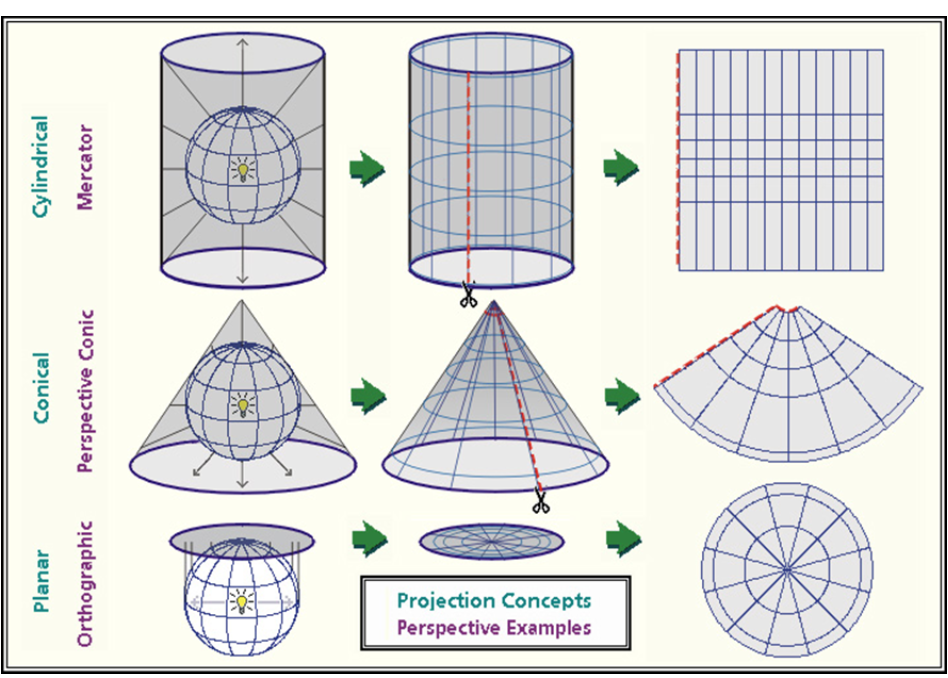
To prepare a map, the earth is first reduced to a globe and then projected onto a flat surface:
The surface of the earth is curved but maps are flat. A Projected Coordinate System (PCS) is a reference system for identifying locations and measuring features on a flat (map) surface. It consists of lines that intersect at right angles, forming a grid. Projected coordinate systems (which are based on Cartesian coordinates) have an origin, an x axis, a y axis, and a linear unit of measure.
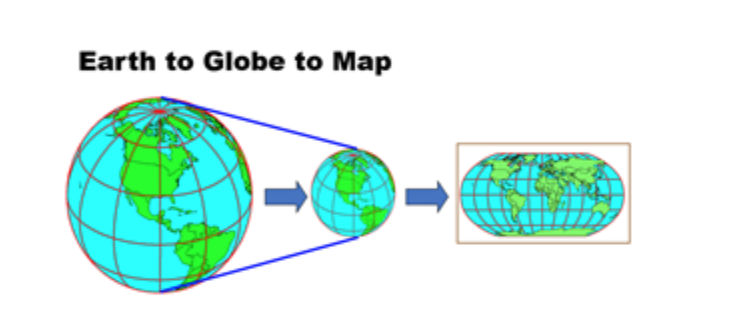
Source: https://kartoweb.itc.nl/geometrics/Map%20projections/mappro.html
Going from a GCS to a PCS requires mathematical transformations:
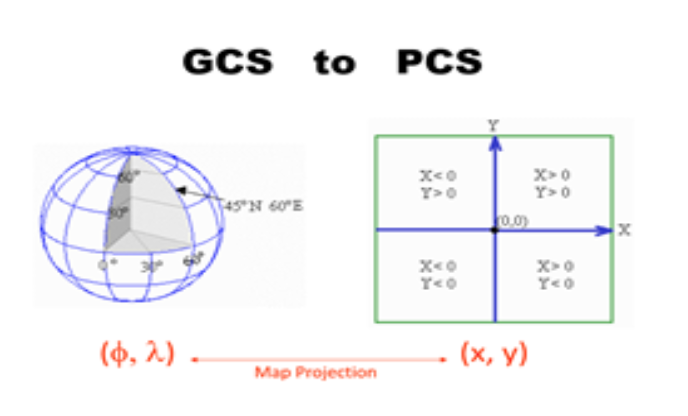
Source: www.mathworks.com
The myriad of projection types can be aggregated into three groups: planar, cylindrical and conical.